这篇笔记介绍lecture14,Binary Relation I。
前置知识
有序对
有序对 < a , b > <a,b> < a , b > a a a b b b a a a b b b
有序对满足
a ≠ b ⇒ < a , b > ≠ < b , a > a \not = b \Rightarrow <a, b> \not = <b, a> a = b ⇒< a , b > =< b , a > < a , b > ≠ < c , d > ⇔ a = c ∧ b = d <a, b> \not = <c, d> \Leftrightarrow a = c \land b = d < a , b > =< c , d >⇔ a = c ∧ b = d
可以通过集合来描述有序对,定义 < a , b > = { { a } , { a , b } } <a,b> = \{\{a\}, \{a, b\}\} < a , b >= {{ a } , { a , b }} a = b a = b a = b < a , b > = { a } <a, b> = \{a\} < a , b >= { a } a ≠ b a \not = b a = b < a , b > = { { a } , { a , b } } <a, b> = \{\{a\}, \{a, b\}\} < a , b >= {{ a } , { a , b }} < b , a > = { { b } , { a , b } } <b, a> = \{\{b\}, \{a, b\}\} < b , a >= {{ b } , { a , b }} { { a } , { a , b } } = { { c } , { c , d } } ⇔ a = c ∧ b = d \{\{a\}, \{a, b\}\} = \{\{c\}, \{c, d\}\} \Leftrightarrow a = c \land b = d {{ a } , { a , b }} = {{ c } , { c , d }} ⇔ a = c ∧ b = d
笛卡尔积
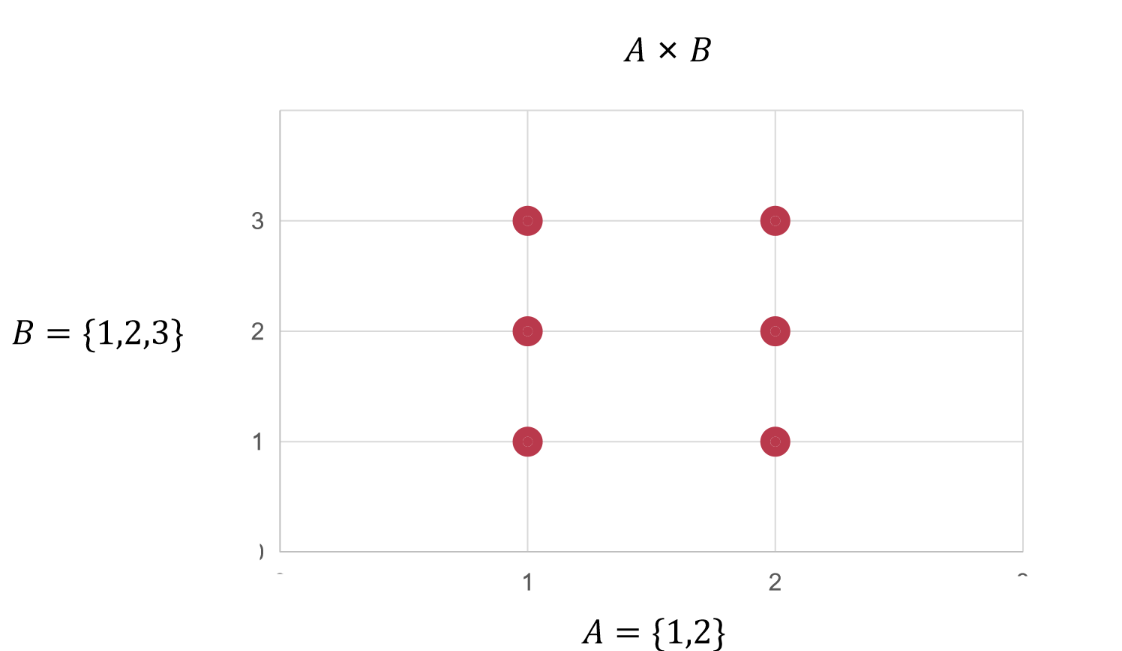
对于集合 A A A B B B A × B A \times B A × B < a , b > <a,b> < a , b > a ∈ A a \in A a ∈ A b ∈ B b \in B b ∈ B A × B = { < a , b > ∣ a ∈ A ∧ b ∈ B } A \times B = \{<a, b>|a \in A \land b \in B\} A × B = { < a , b > ∣ a ∈ A ∧ b ∈ B }
空集和任何集合的笛卡尔积都是空集。
笛卡尔积可以用平面直角坐标系来表示。
两个对象之间的关系称为二元关系(binary relation)。这门课只研究二元关系。
基本概念
如果 A A A B B B A A A B B B A × B A \times B A × B A A A B B B R R R a R b aRb a R b < a , b > <a,b> < a , b > R R R a R b a\cancel{R} b a R b < a , b > <a,b> < a , b > R R R
对于从 A A A B B B R R R R R R d o m ( R ) = { x ∣ ( ∃ y ) ( < x , y > ∈ R ) } dom(R) = \{x|(\exist y)(<x, y>\in R)\} d o m ( R ) = { x ∣ ( ∃ y ) ( < x , y >∈ R )} r a n ( R ) = { y ∣ ( ∃ x ) ( < x , y > ∈ R ) } ran(R) = \{y|(\exist x)(<x, y>\in R)\} r an ( R ) = { y ∣ ( ∃ x ) ( < x , y >∈ R )} f l d ( R ) = d o m ( R ) ∪ r a n ( R ) fld(R) = dom(R) \cup ran(R) f l d ( R ) = d o m ( R ) ∪ r an ( R )
例如,定义集合 A = { 1 , 2 , 3 } A = \{1,2,3\} A = { 1 , 2 , 3 } R = { < x , y > ∣ x ∈ A ∧ y ∈ A ∧ x ∣ y } R = \{<x,y>|x\in A \land y \in A \land x|y\} R = { < x , y > ∣ x ∈ A ∧ y ∈ A ∧ x ∣ y } x ∣ y x|y x ∣ y y y y x x x R = { < 1 , 1 > , < 1 , 2 > , < 1 , 3 > , < 2 , 2 > , < 3 , 3 > } R = \{<1, 1>, <1, 2>, <1, 3>, <2, 2>, <3, 3>\} R = { < 1 , 1 > , < 1 , 2 > , < 1 , 3 > , < 2 , 2 > , < 3 , 3 > } d o m ( R ) = { 1 , 2 , 3 } dom(R) = \{1, 2, 3\} d o m ( R ) = { 1 , 2 , 3 } r a n ( R ) = { 1 , 2 , 3 } ran(R) = \{1, 2, 3\} r an ( R ) = { 1 , 2 , 3 } f l d ( R ) = { 1 , 2 , 3 } fld(R) = \{1, 2, 3\} f l d ( R ) = { 1 , 2 , 3 }
对于任何集合 A A A
恒等关系(identity relation):I A = { < x , x > ∣ x ∈ A } I_A = \{<x, x>|x \in A\} I A = { < x , x > ∣ x ∈ A }
全域关系(universal relation):E A = { < x , y > ∣ x ∈ A ∧ y ∈ A } E_A = \{<x,y>|x \in A \land y \in A\} E A = { < x , y > ∣ x ∈ A ∧ y ∈ A }
空关系(empty relation):N A = ∅ N_A = \varnothing N A = ∅
对于 A A A x x x y y y x N A y x\cancel{N_A}y x N A y x E A y xE_Ay x E A y x = y x=y x = y x I A y xI_Ay x I A y
关系矩阵与关系图
R R R A A A B B B R R R M R = ( m i j ) m × n M_R = (m_{ij})_{m \times n} M R = ( m ij ) m × n
m i j = { 1 i f < a i , b j > ∈ R 0 i f < a i , b j > ∉ R m_{ij} =
\begin{cases}
\text{$1~~if<a_i,b_j>\in R$} \\
\text{$0~~if<a_i,b_j>\not \in R$}
\end{cases} m ij = { 1 i f < a i , b j >∈ R 0 i f < a i , b j > ∈ R 如果 R R R A A A M R M_R M R
例如,如果 A = { 1 , 2 , 3 , 4 } A = \{1, 2, 3, 4\} A = { 1 , 2 , 3 , 4 } R = { < 1 , 1 > , < 1 , 3 > , < 2 , 1 > , < 2 , 3 > , < 2 , 4 > , < 3 , 1 > , < 3 , 2 > , < 4 , 1 > } R = \{<1, 1>, <1, 3>, <2, 1>, <2, 3>, <2, 4>, <3, 1>, <3, 2>, <4, 1>\} R = { < 1 , 1 > , < 1 , 3 > , < 2 , 1 > , < 2 , 3 > , < 2 , 4 > , < 3 , 1 > , < 3 , 2 > , < 4 , 1 > }
M R = [ 1 0 1 0 1 0 1 1 1 1 0 0 1 0 0 0 ] M_{R} =
\begin{bmatrix}
1 & 0 & 1 & 0 \\
1 & 0 & 1 & 1 \\
1 & 1 & 0 & 0 \\
1 & 0 & 0 & 0
\end{bmatrix} M R = 1 1 1 1 0 0 1 0 1 1 0 0 0 1 0 0 类似地,有
M I = [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 ] M_{I} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix} M I = 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 M E = [ 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ] M_{E} =
\begin{bmatrix}
1 & 1 & 1 & 1 \\
1 & 1 & 1 & 1 \\
1 & 1 & 1 & 1 \\
1 & 1 & 1 & 1
\end{bmatrix} M E = 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 M N = [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ] M_N =
\begin{bmatrix}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0
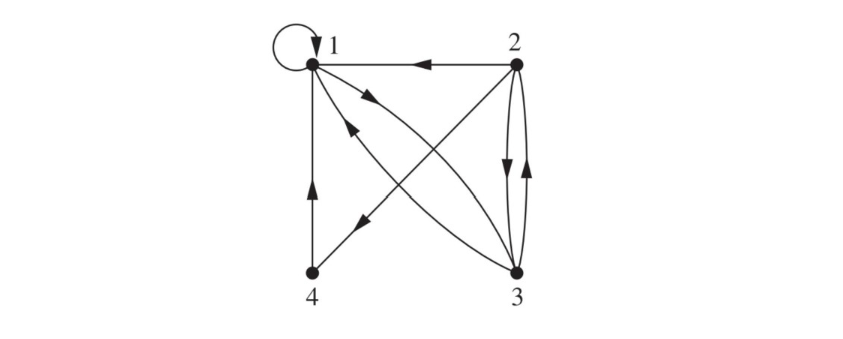
\end{bmatrix} M N = 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 关系还可以通过关系图来表示。在关系图中,顶点代表元素, a R b aRb a R b a a a b b b A = { 1 , 2 , 3 , 4 } A = \{1, 2, 3, 4\} A = { 1 , 2 , 3 , 4 } R = { < 1 , 1 > , < 1 , 3 > , < 2 , 1 > , < 2 , 3 > , < 2 , 4 > , < 3 , 1 > , < 3 , 2 > , < 4 , 1 > } R = \{<1, 1>, <1, 3>, <2, 1>, <2, 3>, <2, 4>, <3, 1>, <3, 2>, <4, 1>\} R = { < 1 , 1 > , < 1 , 3 > , < 2 , 1 > , < 2 , 3 > , < 2 , 4 > , < 3 , 1 > , < 3 , 2 > , < 4 , 1 > }
关系的运算
集合的基本运算在关系中也成立。此外,关系还有一些其它的运算。
R R R A A A B B B R R R R − 1 R^{-1} R − 1 { < a , b > ∣ < b , a > ∈ R } \{<a,b>|<b,a> \in R\} { < a , b > ∣ < b , a >∈ R } M R − 1 = M R T M_{R^{-1}} = M_R^T M R − 1 = M R T
R R R A A A B B B S S S B B B C C C R R R S S S S ∘ R S \circ R S ∘ R { < x , y > ∣ ( ∃ z ) ( < x , z > ∈ R ∧ < z , y > ∈ S ) } \{<x, y>|(\exist z)(<x,z>\in R \land <z,y>\in S)\} { < x , y > ∣ ( ∃ z ) ( < x , z >∈ R ∧ < z , y >∈ S )} M R = ( r i j ) M_R = (r_{ij}) M R = ( r ij ) M S = ( s i j ) M_S = (s_{ij}) M S = ( s ij ) M S ∘ R = M R ⊙ M S = ( w i j ) M_{S \circ R} = M_R \odot M_S = (w_{ij}) M S ∘ R = M R ⊙ M S = ( w ij ) ⊙ \odot ⊙ w i j = ∨ k = 1 n ( r i k ∧ s k j ) w_{ij} = \lor _{k=1}^n(r_{ik} \land s_{kj}) w ij = ∨ k = 1 n ( r ik ∧ s kj )
[ 1 0 1 0 1 1 ] ⊙ [ 1 1 0 0 0 1 ] = [ 1 1 0 1 ] \begin{bmatrix}
1 & 0 & 1 \\
0 & 1 & 1
\end{bmatrix}
\odot
\begin{bmatrix}
1 & 1 \\
0 & 0 \\
0 & 1 \\
\end{bmatrix}
=
\begin{bmatrix}
1 & 1 \\
0 & 1
\end{bmatrix} [ 1 0 0 1 1 1 ] ⊙ 1 0 0 1 0 1 = [ 1 0 1 1 ] 其中有
w 11 = ( 1 ∧ 1 ) ∨ ( 0 ∧ 0 ) ∨ ( 1 ∧ 0 ) = 1 w_{11} = (1 \land 1) \lor (0 \land 0) \lor (1 \land 0) = 1 w 11 = ( 1 ∧ 1 ) ∨ ( 0 ∧ 0 ) ∨ ( 1 ∧ 0 ) = 1 w 12 = ( 1 ∧ 1 ) ∨ ( 0 ∧ 0 ) ∨ ( 1 ∧ 1 ) = 1 w_{12} = (1 \land 1) \lor (0 \land 0) \lor (1 \land 1) = 1 w 12 = ( 1 ∧ 1 ) ∨ ( 0 ∧ 0 ) ∨ ( 1 ∧ 1 ) = 1 w 21 = ( 0 ∧ 1 ) ∨ ( 1 ∧ 0 ) ∨ ( 1 ∧ 0 ) = 0 w_{21} = (0 \land 1) \lor (1 \land 0) \lor (1 \land 0) = 0 w 21 = ( 0 ∧ 1 ) ∨ ( 1 ∧ 0 ) ∨ ( 1 ∧ 0 ) = 0 w 22 = ( 0 ∧ 1 ) ∨ ( 1 ∧ 0 ) ∨ ( 1 ∧ 0 ) = 1 w_{22} = (0 \land 1) \lor (1 \land 0) \lor (1 \land 0) = 1 w 22 = ( 0 ∧ 1 ) ∨ ( 1 ∧ 0 ) ∨ ( 1 ∧ 0 ) = 1
关系的逆和合成有下面这些性质。
d o m ( R − 1 ) = r a n ( R ) dom(R^{-1}) = ran(R) d o m ( R − 1 ) = r an ( R ) r a n ( R − 1 ) = d o m ( R ) ran(R^{-1}) = dom(R) r an ( R − 1 ) = d o m ( R ) ( R − 1 ) − 1 = R (R^{-1})^{-1} = R ( R − 1 ) − 1 = R ( S ∘ R ) − 1 = R − 1 ∘ S − 1 (S \circ R)^{-1} = R^{-1} \circ S^{-1} ( S ∘ R ) − 1 = R − 1 ∘ S − 1 ( R ∘ S ) ∘ Q = R ∘ ( S ∘ Q ) (R \circ S) \circ Q = R \circ (S \circ Q) ( R ∘ S ) ∘ Q = R ∘ ( S ∘ Q ) R 1 ∘ ( R 2 ∪ R 3 ) = R 1 ∘ R 2 ∪ R 1 ∘ R 3 R_1 \circ (R_2 \cup R_3) = R_1 \circ R_2 \cup R_1 \circ R_3 R 1 ∘ ( R 2 ∪ R 3 ) = R 1 ∘ R 2 ∪ R 1 ∘ R 3 ( R 1 ∪ R 2 ) ∘ R 3 = ( R 1 ∪ R 3 ) ∘ ( R 2 ∪ R 3 ) (R_1 \cup R_2) \circ R_3 = (R_1 \cup R_3) \circ (R_2 \cup R_3) ( R 1 ∪ R 2 ) ∘ R 3 = ( R 1 ∪ R 3 ) ∘ ( R 2 ∪ R 3 ) R 1 ∘ ( R 2 ∩ R 3 ) ⊆ ( R 1 ∘ R 2 ) ∩ ( R 1 ∘ R 3 ) R_1 \circ (R_2 \cap R_3) \subseteq (R_1 \circ R_2) \cap (R_1 \circ R_3) R 1 ∘ ( R 2 ∩ R 3 ) ⊆ ( R 1 ∘ R 2 ) ∩ ( R 1 ∘ R 3 ) ( R 1 ∩ R 2 ) ∘ R 3 ⊆ ( R 1 ∘ R 3 ) ∩ ( R 2 ∘ R 3 ) (R_1 \cap R_2) \circ R_3 \subseteq (R_1 \circ R_3) \cap (R_2 \circ R_3) ( R 1 ∩ R 2 ) ∘ R 3 ⊆ ( R 1 ∘ R 3 ) ∩ ( R 2 ∘ R 3 )
对于集合 A A A R R R n ∈ N n \in N n ∈ N R R R n n n R n R^n R n
R n = { I A , n = 0 R n ∘ R , n ≠ 0 R^n =
\begin{cases}
\text{$I_A,~~n = 0$} \\
\text{$R^n \circ R,~~n \not = 0$}
\end{cases} R n = { I A , n = 0 R n ∘ R , n = 0 对于关系的幂,有
R m ∘ R n = R m + n R^m \circ R^n = R^{m + n} R m ∘ R n = R m + n ( R m ) n = R m n (R^m)^n = R^{mn} ( R m ) n = R mn A A A R R R A A A s s s t t t s ≠ t s \not = t s = t R s = R t R^s = R^t R s = R t
关系的划分
关系的性质
如果 ( ∀ a ) ( a ∈ A → a R a ) (\forall a)(a \in A \rightarrow aRa) ( ∀ a ) ( a ∈ A → a R a ) R R R ( ∀ a ) ( ∀ b ) ( ( a ∈ A ∧ b ∈ A ∧ a R b ) → b R a ) (\forall a)(\forall b)((a \in A \land b \in A \land aRb) \rightarrow bRa) ( ∀ a ) ( ∀ b ) (( a ∈ A ∧ b ∈ A ∧ a R b ) → b R a ) R R R ( ∀ a ) ( ∀ b ) ( ∀ c ) ( ( a ∈ A ∧ b ∈ A ∧ c ∈ A ∧ a R b ∧ b R c ) → a R c ) (\forall a)(\forall b)(\forall c)((a \in A \land b \in A \land c \in A \land aRb \land bRc) \rightarrow aRc) ( ∀ a ) ( ∀ b ) ( ∀ c ) (( a ∈ A ∧ b ∈ A ∧ c ∈ A ∧ a R b ∧ b R c ) → a R c ) R R R
对称关系等价于 R − 1 = R R^{-1} = R R − 1 = R M R = M R T M_R = M_R^T M R = M R T
如果 R 1 , R 2 R_1,R_2 R 1 , R 2 R 1 − 1 , R 1 ∪ R 2 , R 1 ∩ R 2 R_1^{-1},R_1 \cup R_2,R_1 \cap R_2 R 1 − 1 , R 1 ∪ R 2 , R 1 ∩ R 2 R 1 , R 2 R_1��,R_2 R 1 , R 2 R 1 − 1 , R 1 ∪ R 2 , R 1 ∩ R 2 R_1^{-1},R_1 \cup R_2,R_1 \cap R_2 R 1 − 1 , R 1 ∪ R 2 , R 1 ∩ R 2 R 1 , R 2 R_1,R_2 R 1 , R 2 R 1 − 1 , R 1 ∩ R 2 R_1^{-1},R_1 \cap R_2 R 1 − 1 , R 1 ∩ R 2
集合的划分(partition)是指将集合划分为不相交的、非空的子集。更正式地说,对于一个非空集合 A A A π \pi π
∅ ∉ π \varnothing \notin \pi ∅ ∈ / π ( ∀ x ) ( x ∈ π → x ⊆ A ) (\forall x)(x \in \pi \rightarrow x \subseteq A) ( ∀ x ) ( x ∈ π → x ⊆ A ) ∪ π = A \cup \pi = A ∪ π = A ( ∀ x ) ( ∀ y ) ( ( x ∈ π ∧ y ∈ π ∧ x ≠ y ) → x ∩ y = ∅ ) (\forall x)(\forall y)((x \in \pi \land y \in \pi \land x \not = y) \rightarrow x \cap y = \varnothing) ( ∀ x ) ( ∀ y ) (( x ∈ π ∧ y ∈ π ∧ x = y ) → x ∩ y = ∅ )
则 π \pi π A A A
对于 A A A π \pi π R R R a , b a,b a , b a R b aRb a R b R = { < a , b > ∣ ( ∃ π 0 ) ( π 0 ∈ π ∧ a ∈ π 0 ∧ b ∈ π 0 ) } R = \{<a,b>|(\exist \pi_0)(\pi_0 \in \pi \land a \in \pi_0 \land b \in \pi_0)\} R = { < a , b > ∣ ( ∃ π 0 ) ( π 0 ∈ π ∧ a ∈ π 0 ∧ b ∈ π 0 )}
等价关系
如果某个关系是自反的、对称的、传递的,则这个关系是等价关系(equivalence relation)。若 R R R A A A x ∈ A x \in A x ∈ A x x x [ x ] R = { y ∣ y ∈ A ∧ x R y } [x]_R = \{y|y \in A \land xRy\} [ x ] R = { y ∣ y ∈ A ∧ x R y }
对于集合 A A A R R R A A A A A A A / R A/R A / R A / R = { y ∣ ( ∃ x ) ( x ∈ A ∧ y = [ x ] R ) } A/R = \{y|(\exist x)(x \in A \land y = [x]_R)\} A / R = { y ∣ ( ∃ x ) ( x ∈ A ∧ y = [ x ] R )} A / R A/R A / R A A A
等价关系与划分
对于 A A A π \pi π R = { < a , b > ∣ ( ∃ π 0 ) ( π 0 ∈ π ∧ a ∈ �π 0 ∧ b ∈ π 0 ) } R = \{<a,b>|(\exist \pi_0)(\pi_0 \in \pi \land a \in \pi_0 \land b \in \pi_0)\} R = { < a , b > ∣ ( ∃ π 0 ) ( π 0 ∈ π ∧ a ∈ π 0 ∧ b ∈ π 0 )}
反过来,对于 A A A R R R A / R A/R A / R A A A